<본 포스팅은 강좌가 아닙니다.>
앞 포스팅에서 난반사광에서 람베르트 모델을 썼다.
(정반사광에서는 퐁 모델 썼었지..)
람베르트 모델은 표면 법선과 입사광의 코사인 값이
난반사광의 양이라고 했다.
툰셰이더는 기존 난반사광의 양처럼 코사인 곡선이 부드럽지 않게
0.2단위로 올림을 하면 툰셰이더 값이 나온다.

빨간선처럼 각진 코사인의 난반사광을 적용하면 된다. 올림을 통해서..
자세한 구현 내용은 아래 있다.

이전 장에서는 계속 월드행렬, 뷰행렬, 투영행렬로
순차적으로 곱해서 픽셀셰이더로 넘겼는데
이번 장부터는 월드뷰투영행렬을 미리 합쳐둔 행렬을 사용한다.
불필요한 연산을 피하기 위해서다.
하지만 난반사광을 구할려면 월드행렬이 필요했다.
이는 월드행렬의 역행렬로 지역공간으로 변환해서 해결한다.
모든 변수들을 동일한 공간에서 시작할수있게 만들어준다.
위 사진에서 WorldViewProjMatrix와 InverseWorldMatrix가 그것이다.

초록색 주석부분보면 라이트의 월드위치를 역행렬로 지역공간으로 바꿔준다.
정점의 법선과 Dot 내적을 통해 얻는 난반사의 양을
diffuse 변수에 저장해서 PS로 보내주는 모습이다.
픽셀 셰이더에서는 버텍스셰이더에서 받아온 값을
0~1 사이로 바꿔주는 Saturate 함수
그리고 0.2단위로 올림하는 ceil(diffuse * 5) / 5.0f;를 ceil함수를 사용한다.
diffuse가 0~1의 값이니까 곱하기 5는 0~5의 값이다.
ceil함수로 0.2가 나와도 0이 되는 즉, 0, 1, 2, 3, 4, 5로 올림이 된다.
그 올림된 수를 나누기 5로 나누면 0.0, 0.2, 0.4, 0.6, 0.8, 1.0이 된다.
그런 알고리즘이다.


셰이더 프로그래밍 입문서 책 내용과 별개로
텍스쳐를 추가해봤는데 카툰 형식에는 비교적 어울리지 않았다.
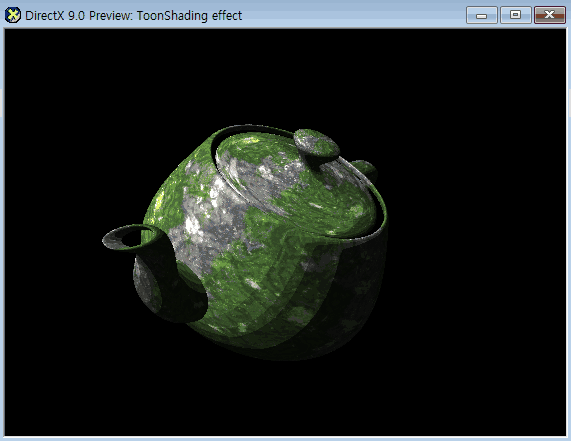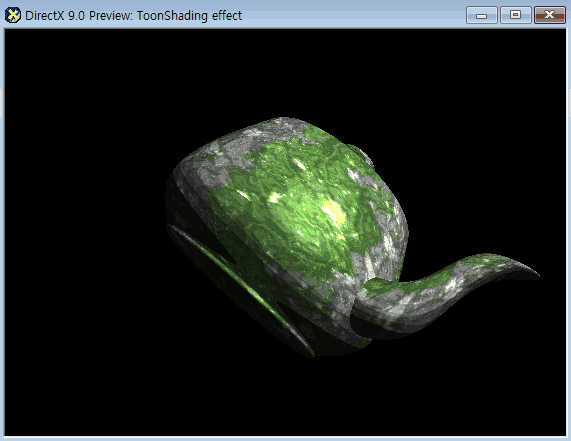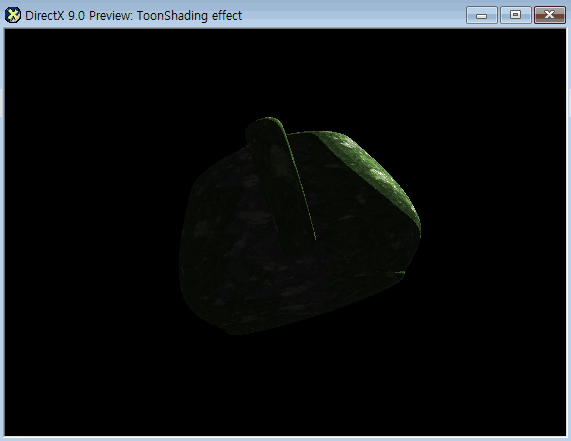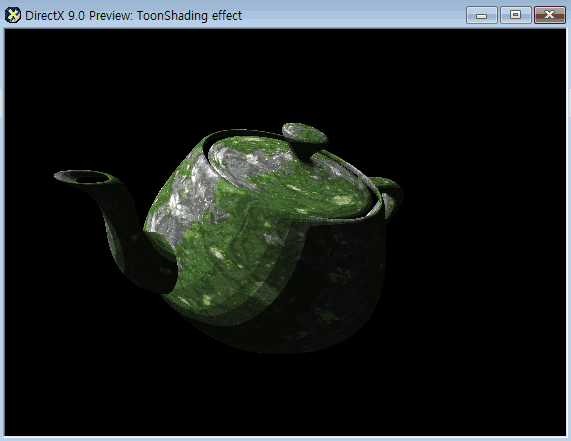
예시로는 보더랜드 그래픽을 보면 텍스쳐를 사용하긴 했지만
주로 단색을 사용했다는 점이다.

또한 책 내용과 별개로 정반사광도
복습할겸 툰셰이더에 추가해보았다.
아래는 최종 결과
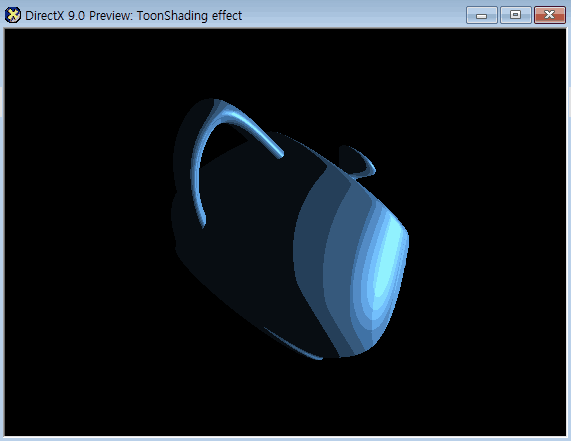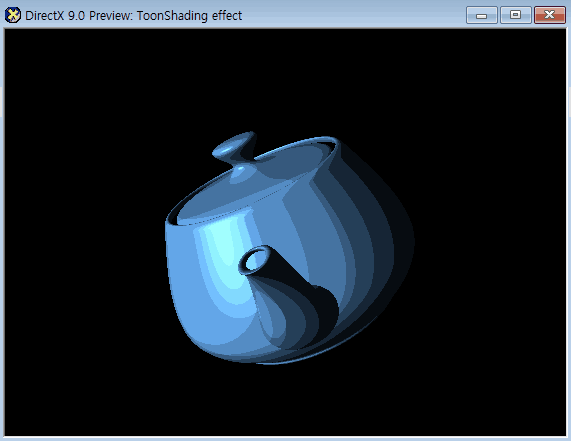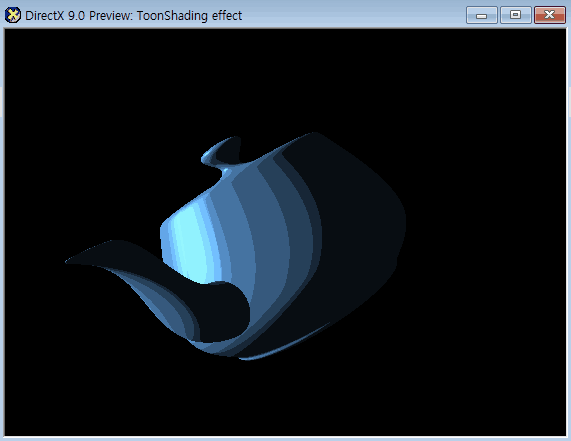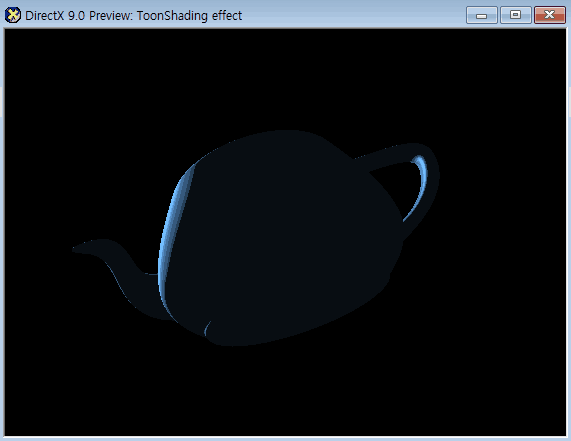
아래는 풀 소스코드이다.
//VS
struct VS_INPUT
{
float4 mPosition : POSITION;
float3 mNormal : NORMAL;
};
struct VS_OUTPUT
{
float4 mPosition : POSITION;
float3 mDiffuse : TEXCOORD1;
//정반사
float3 mViewDir : TEXCOORD2;
float3 mReflection : TEXCOORD3;
};
float4x4 gWorldViewProjMatrix;
float4x4 gInvWorldMatrix;
float4 gWorldLightPos;
float4 gWorldCamPos;
VS_OUTPUT vs_main(VS_INPUT Input)
{
VS_OUTPUT Output;
//바로 화면 뷰포트 행렬 변환
Output.mPosition= mul(Input.mPosition, gWorldViewProjMatrix);
//월드 역행렬로 라이트 위치 지역공간 로 바꿔줌
float3 objectlightPos = mul(gWorldLightPos, gInvWorldMatrix);
//카메라 캠 위치도 지역공간으로 바꿔줌
float3 viewDir = mul(gWorldCamPos, gInvWorldMatrix);
Output.mViewDir=viewDir;
float3 lightDir = normalize(Input.mPosition.xyz-objectlightPos);
Output.mUV = Input.mUV;
Output.mDiffuse = dot(-lightDir, normalize(Input.mNormal));
Output.mReflection = reflect(lightDir, Input.mNormal);
return Output;
}
//PS
struct PS_INPUT
{
float3 mDiffuse : TEXCOORD1;
float3 mViewDir : TEXCOORD2;
float3 mReflection : TEXCOORD3;
};
float3 gSurfaceColor;
float4 ps_main(PS_INPUT Input) : COLOR
{
float3 diffuse = saturate(Input.mDiffuse);
float3 reflection = normalize(Input.mReflection);
float3 viewDir = normalize(Input.mViewDir);
float3 specular=0;
if(diffuse.x > 0.0f)
{
specular = saturate(dot(reflection, viewDir));
specular = pow(specular, 10.0f);
}
diffuse = ceil(diffuse * 5) / 5.0f;
specular = ceil(specular *5)/5.0f;
float3 ambient= float3(0.1f,0.1f,0.1f);
return float4(gSurfaceColor*(ambient+specular+diffuse.xyz),1.0f);
}'STUDY > Shader Programming' 카테고리의 다른 글
| 셰이더 프로그래밍 - AMD RenderMonkey 사용해서 쉐이더 공부를 해보자6 (환경 매핑, 입방체 매핑) (0) | 2021.12.20 |
|---|---|
| 셰이더 프로그래밍 - AMD RenderMonkey 사용해서 쉐이더 공부를 해보자5 (법선 매핑) (0) | 2021.12.20 |
| 셰이더 프로그래밍 - AMD RenderMonkey 사용해서 쉐이더 공부를 해보자3 (디퓨즈/ 스페큘러 매핑) (0) | 2021.12.17 |
| 셰이더 프로그래밍 - AMD RenderMonkey 사용해서 쉐이더 공부를 해보자2 (기초 조명 셰이더 - 난반사광, 정반사광) (0) | 2021.12.17 |
| 셰이더 프로그래밍 - AMD RenderMonkey 사용해서 쉐이더 공부를 해보자 (텍스쳐 적용 tex2d()함수) (0) | 2021.12.16 |