3D 프로그래밍 수학에서 중요한 것은 벡터의 내적이다.
벡터의 내적은 왜 사용할까..?
1. 두 벡터의 사이각을 구하기 위해
2. 두 벡터를 분해해 수직 및 평행한 벡터를 얻기 위해
3. 두 벡터가 가리키는 방향의 차이를 알기 위해 사용한다.
벡터의 외적은 두 벡터의 직교인 벡터를 구할 수 있다.
내적과 외적은 벡터를 마치 수처럼 곱한다는 개념이다.
결과로는 내적은 스칼라 값의 결과, 외적은 벡터값의 결과이다.

위 공식처럼 각 성분을 곱해서 더하는 것이다. 결과값은 스칼라이다.
만일 ab가 = 0 직교, ab > 0 면 각도는 예각, ab < 0 면 각도는 둔각
예를 들어 u(1,2,3)v(-4,0,-1)일때 둘의 내적은
(1*-4)+(2*0)+(3*-1)=-7 이니 0보다 작으니까 둘 사이는 둔각이다.
정규화된 벡터 ab라면 cos만 남게되면.
ab 직각을 이루고 있다면 내적값은 0이 되고
다른 방향을 보고 있다면 내적값은 -1이되고
같은 방향을 보고 있다면 내적값은 1이 된다.
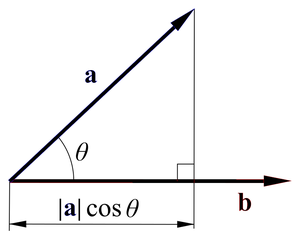
이는 게임에서는 내적을 이용해 같은 곳을 바라보는지 다른 방향을 바라보는지 유추 가능하다.
내적으로 사이각을 구하는 방법은
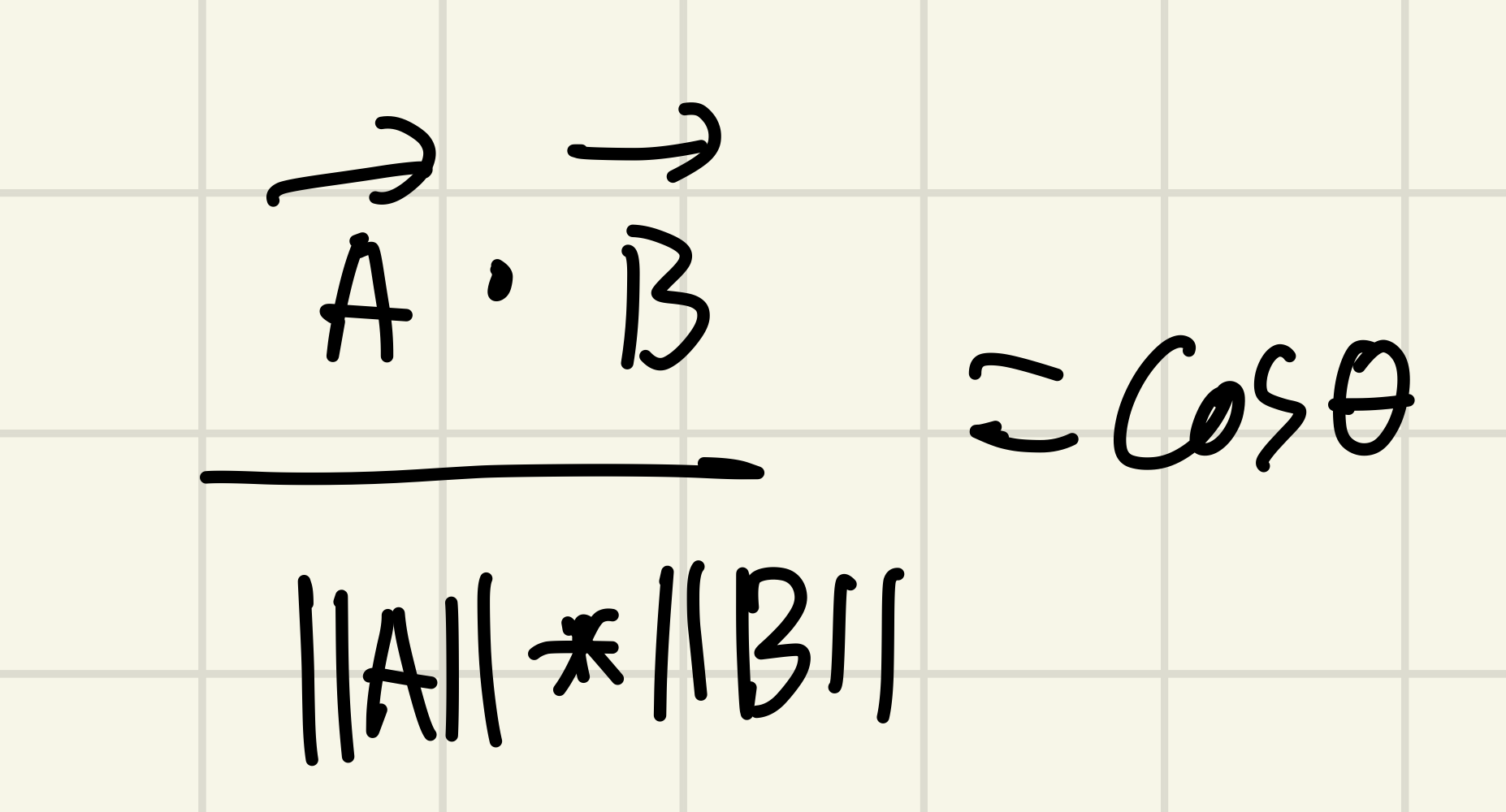
코사인 식을 활용해서 도출한다. 벡터의 길이 분의 내적인 공식이다.
벡터의 길이는 피타고라스의 정리를 사용한다.
그러면 코사인 세타값을 얻고 arccos이나 cos-1 함수를 사용해
알고 있는 코사인 세타 값으로 각을 구할 수 있다.
아래는 함수로 구현한 것이다.
float AngleFromCosine( D3DXVECTOR2& p1, D3DXVECTOR2& p2 )
{
// a^2 = b^2 + c^2 - 2b cos A
return acos( (p1.x * p2.x + p1.y * p2.y) / (D3DXVec2Length( &p1 ) * D3DXVec2Length( &p2 )) );
}
이는 빛의 강도 조명연산, 쉐도우 연산에 적용될수 있다.
-------------------------
외적은 마찬가지로 곱하지만 결과값은 벡터이다.
외적은 두 벡터에 서로 직교하는 벡터를 반환한다.
따라서 면을 이루는 벡터를 이용해 직교하는 벡터 즉,
면의 법선벡터를 구하는데에 사용할 수 있다.
교환법칙이 성립하지 않기 때문에 교환할경우 방향이 바뀐다.
교환법칙이 성립하지않는 예시)
x=(2,1,3) y=(2,0,0) 일때 아래 공식을 적용하면
x X y 는 (0,6,-2)이고 y X x 는 (0,-6,2) 가 나온다.

'STUDY > Game Mathematics' 카테고리의 다른 글
| DirectX11 - Fixed Angle(고정 각), Euler Angle(오일러 각), Quaternion(사원수) 정리 (0) | 2022.03.25 |
|---|---|
| 행렬 Matrix - 상등, 덧셈, 곱셈, 전치, 단위, 행렬식, 역행렬, 소행렬식 계산 방법 (0) | 2021.12.16 |
| 삼각함수 표 (0) | 2021.11.01 |
| DirectX11 3D - 이동 행렬, 신축 행렬(스케일), 회전 행렬 (0) | 2021.10.28 |