-행렬의 상등, 덧셈, 스칼라 곱셈, 뺄셈
행렬의 상등 : 두 행렬의 행수와 열수가 같음
행렬의 덧셈 : 행수와 열수가 같은 행렬 들만 덧셈 가능하다.
행렬의 스칼라 곱셈 : 모든 성분에 그 스칼라를 곱셈함
행렬의 뺄셈 : 곱셈과 행렬 덧셈으로 정의함
-행렬 곱셈
행렬의 곱셈은 교환 법칙이 성립하지 않음 AB의 곱이 정의되려면
A의 열 수가 B의 행수와 일치해야 함 2X3 * 3X2 내항 일치라고 함
행렬의 곱은 내적의 연속이다.
고로 2차원 벡터와 3차원 벡터의 내적을 취할 수 없다.
-행렬의 전치 transpose

주어진 행렬의 행들과 열들을 맞바꾼것을 의미한다.
T로 표시한다. 다음과 같은 유용한 속성이 있음
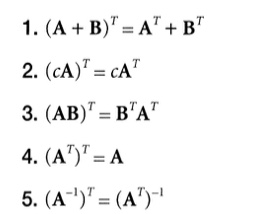
(AB)T = BT*AT 세번째 성질을 보면 곱셈은 순서가 바뀐다.
-단위행렬 identity
10 100 1000
01 010 0100
001 0010
0001
단위행렬은 대각선 1 나머지 0인 정방 행렬이다.
1의 행렬 버전, 곱해도 행렬이 변하지 않음
-역행렬 inverse
오직 정방 행렬만이 역행렬을 가지지만 모든 정방 행렬이 역행렬을 가지는 건 아님
역행렬이 있는 행렬을 가리켜 가역 행렬이라고 부르고 없으면 특이 행렬이라고 함
A형렬이 직교행렬이면 A의 역행렬은 A의 전치행렬과 같다.
대부분의 DirectX는 직교행렬을 쓰기 때문에
역행렬대신에 전치행렬을 쓰기도한다.
역행렬 구하는 공식은 아래와 같다.
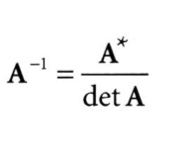
detA는 행렬식이다. A*는 딸림행렬 혹은 수반행렬(adjoint matrix)이다.
최종적으로 공식은 이렇게 된다.

행렬식이 0이면 역행렬이 없다는 뜻이며 행렬식은
역행렬의 유무를 따지는데에 사용한다.
그럼 아래서 부터 행렬식과 딸림행렬(여인수 행렬의 전치)
를 구하는 방법을 알아보자.
-행렬식(determinant)
행렬식은 역행렬을 구할 수 있는지 판별하는 식으로
3x3까지는 사러스법칙으로 구할 수 있지만
4x4 이상은 라이프니츠가 만든 소행렬식이나 크레마공식을 사용해야 한다.
-행렬식(determinant) - 소행렬

위 그림을 보면 소행렬은 한 행과 열을 잡아 그 부분을 뺀
나머지가 소행렬이 된다는 것을 볼 수 있다.
모든 행과 열을 잡아 그 부분을 빼서 소행렬식을 계산하면
마이너 행렬을 구할 수있다. 모든 행과 열의 소행렬식 모음집.
소행렬 식에 + - + - (짝수면 + 홀수면 -) 부호를 붙인 것을
여인수(confactor)라고 한다.
마이너 행렬 -> 여인수 행렬 -> 전치하면 딸림, 수반행렬이된다.
아래는 순서대로 행렬의 소행렬 정의를 적용한 2x2, 3x3, 4x4 행렬식이다.
재귀적으로 정의된다. det로 표기함
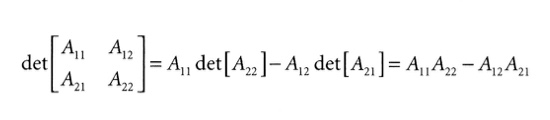


만약에 3X3 행렬식을 구한다고 하면
위의 행렬식을 보며 반대로 접근하면 된다.
소행렬식 계산
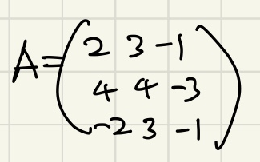
A 같은 임의의 행렬이 있다고 했을때
임의의 행 또는 열을 잡아 사용하면 행렬식을 얻을 수 있다.
->1행기준

->1열기준

둘다 마찬가지로 20이 나온다.
어디 기준으로 행렬식을 구하든 같은 값이 나오기 때문에
행렬식을 구하는데에는 계산이 편한 행 또는 열 기준으로 구하는게 편하다.
아무튼 이 행렬은 0이 아니여서
역행렬이 존재한다. 그럼 역행렬을 구해보자.
역행렬 도출

'STUDY > Game Mathematics' 카테고리의 다른 글
| DirectX11 - Fixed Angle(고정 각), Euler Angle(오일러 각), Quaternion(사원수) 정리 (0) | 2022.03.25 |
|---|---|
| 삼각함수 표 (0) | 2021.11.01 |
| 벡터의 내적과 외적 (0) | 2021.10.28 |
| DirectX11 3D - 이동 행렬, 신축 행렬(스케일), 회전 행렬 (0) | 2021.10.28 |